Solution
- The function given is:
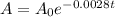
- We have been given:
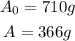
- We are required to find the time for the radioactive substance to decay. That means we need to find the value of t in the equation.
- Thus, we have that:

Final Answer
The answer is 236.65 years