Question

Make a 2 column proofplease make it simple like JK is parallel to NM(given)

Answer 1

Explanation:

Since L is the midpoint of JM, then JL = LM.

Therefore,

Statement: JL = LM

Reason: L is the midpoint of JM

The lines JK and NM are parrallel; therefore, by the alternate interior angles theorem,

`\angle LJK=\angle LMN`

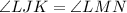
Furthermore, since ∠JLK and ∠MLN are vertical angles,

`∠JLK=∠MLN`

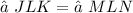
Now since ∠JLK = ∠MLN, ∠LJK = ∠LMN, and JL = LM, then by ASA postulate

`\boxed{△JKL=△MNL.}`

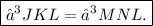
Hence, our proof is complete!