We have a line with slope -2. A parallel line would have a slope of -2 too, and a line perpendicular to it will have a slope of 1/2.
If line A is perpendicular to B, the slope of B is the inverse multiplicative of the sloe of A. That is why a line perpendicular to the one with slope -2 is 1/2:

Now we know the slopes for both cases: parallel and perpendicular. If the slope is different to -2 or 1/2, we can say that is not parallel nor perpendicular to the line given.
Let's evaluate the slope of the line that passes through points (-2, 1) and (6,5).
The slope is given by the following formula:

Where x₁ and y₁ are the x and y-coordinates of the first point (-2 and 1), and x₂ and y₂ are the x and y coordinates of the second point (6 and 5, respectively).
Replacing values:
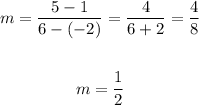
The slope of the line passing through the points given is 1/2, then, according to what was said above, that line is perpendicular to a line with slope -2.