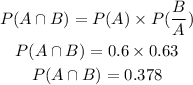Question

Given P(A) = 0.6, P(B) = 0.42 and P(B|A) = 0.63, find the value ofP(An B), rounding to the nearest thousandth, if necessary

Answer 1

Here, we are given;

P(A)=0.6

P(B)=0.42

P(B/A)=0.63

We have to find;

`P(A\cap B)`

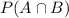
Now,

`P((B)/(A))=(P(A\cap B))/(P(A))`

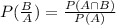
This is the formula for finding conditional probability.

From here,we can see that we have values of P(B/A) and P(A) and we can easily find P(Aand B) from here.

Since P(A)>0 so we can use this formula.

Therefore,

`\begin{gathered} P(A\cap B)=P(A)* P((B)/(A)) \\ P(A\cap B)=0.6*0.63 \\ P(A\cap B)=0.378 \end{gathered}`