ANSWER
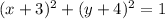
Step-by-step explanation
We want to write the equation of the circle in vertex form:
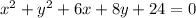
The first step is to group the x terms and y terms together and take the constant to the right-hand side of the equality sign:
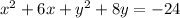
Now, complete the square for the x terms:
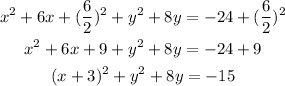
Repeat the process for the y terms:
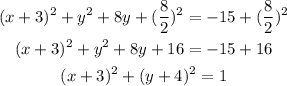
That is the equation of the circle in vertex form.