Question

2. The area of the base of the cone is 64π cm2 and the altitude is 6 cm. Calculate the cone: (a) the length of the constituent;(b) the area of the lateral area of the cone; c) the volume.

Answer 1

Answer: We have to calculate the (i) volume and (ii) the surface area of the cone:

`\begin{gathered} A=\pi r^2+\pi rl\rightarrow(1) \\ \\ V=\pi r^2(h)/(3)\rightarrow(2) \end{gathered}`

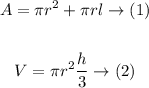
The formula (1) is for the lateral surface of the cone and the formula (2) is for the volume of the cone, the unknowns are determined as follows:

`\begin{gathered} r=\sqrt{(64\pi)/(\pi)}=8cm \\ \\ r=8cm \\ \\ l=√(r^2+h^2)=√((8cm)^2+(6cm)^2) \\ \\ l=√(100)=10 \\ \\ l=10 \end{gathered}`

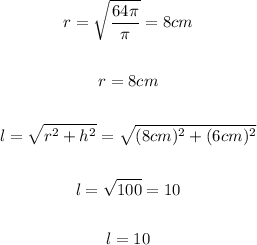
Therefore the volume and the lateral surface area is calculated as follows:

`\begin{gathered} \begin{equation*} A=\pi r^2+\pi rl \end{equation*} \\ \\ A=\pi(8)^2+\pi(8)(10) \\ \\ A=144\pi cm^2\Rightarrow(x) \\ \\ \begin{equation*} V=\pi r^2(h)/(3) \end{equation*} \\ \\ V=\pi(8cm)^2(6cm)/(3) \\ \\ V=128\pi cm^3\Rightarrow(y) \end{gathered}`

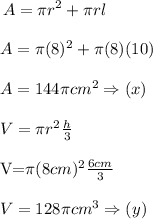
Therefore x and y are the answers.