Question

Lukalu is rappelling off a cliff. The parametric equations that describe her horizontal and vertical position as a function of time are x ( t ) = 8 t and y ( t ) = − 16 t 2 + 100 and . How long does it take her to reach the ground? How far away from the cliff is she when she lands? Remember to show all of the steps that you use to solve the problem.

Answer 1

Now the ground is assumed to be 0, so we have that

`y(t)=0`

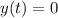
So, that means we have

`\begin{gathered} y(t)=-16t^2+100 \\ 0=-16t^2+100 \\ 16t^2=100 \\ t^2=(100)/(16) \\ t=\sqrt{(100)/(16)} \\ t=(10)/(4) \\ t=2.5\text{ seconds } \end{gathered}`

Now, we have found t, which is how long it takes to get to the ground, you can plug it into x(t) to find the horizontal distance travelled, we have

`\begin{gathered} x(t)=8t \\ x(2.5)=8*2.5 \\ =20\text{ feet } \end{gathered}`

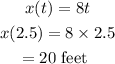
Hence it takes her 2.5 seconds to reach the ground

And she is 20 feet away from the cliff