Question

Solve by substitution when equations are solved for a variable. y = x +3 y = 2x + 12

Answer 1

`\begin{cases}y=x+3\Rightarrow\text{ Equation 1} \\ y=2x+12\Rightarrow\text{ Equation 2}\end{cases}`

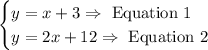
To solve the given system of equations by substitution method, we can do the following steps:

Step 1: We substitute the y-value of one equation into the other equation. For example, we replace the value of y from Equation 1 into Equation 2.

`\begin{gathered} y=2x+12\Rightarrow\text{ Equation 2} \\ x+3=2x+12 \end{gathered}`

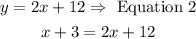
Step 2: We solve for x the resulting equation.

`\begin{gathered} x+3=2x+12 \\ \text{ Subtract 3 from both sides} \\ x+3-3=2x+12-3 \\ x=2x+9 \\ \text{ Subtract 2x from both sides} \\ x-2x=2x+9-2x \\ -x=9 \\ \text{ Multiply by -1 from both sides} \\ -x\cdot-1=9\cdot-1 \\ \boldsymbol{x=-9} \end{gathered}`

Step 3: We replace the value of x in any of the initial equations. For example, in Equation 1:

`\begin{gathered} y=x+3 \\ y=-9+3 \\ $$\boldsymbol{y=-6}$$ \end{gathered}`

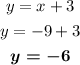
Therefore, the solution of the given system of equations is the ordered pair (-9,-6).