Question

Given f(x)=2^(x+1) -3, what is f^ –1(x)? (It is asking for the inverse).A. f ^–1(x) = log2(x + 3) – 1B. f ^–1(x) = log2(x – 1) + 3C. f ^–1(x) = log2(x + 1) – 3D. f ^–1(x) = log2(x – 3) + 1

Answer 1

Given the function:

`f(x)=2^((x+1))-3`

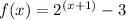
You can find its inverse as follows:

1. Rewrite the function using:

`y=f(x)`

Then:

`y=2^((x+1))-3`

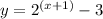
2. Solve for "x":

- Add 3 to both sides of the equation:

`y+3=2^((x+1))-3+3`

`y+3=2^((x+1))`

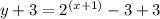
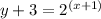
- Apply logarithm to both sides:

`log(y+3)=log(2)^((x+1))`

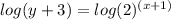
- Apply the Power Property for Logarithms:

`log(m)^n=nlog(m)`

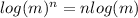
Then:

`log(y+3)=(x+1)log(2)^`

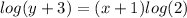
- Divide both sides of the equation by:

`log(2)`

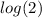
You get:

`(log(y+3))/(log(2))=(x+1)/(log(2))`
`(log(y+3))/(log(2))=x+1`

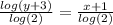
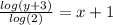
- Subtract 1 from both sides:

`(log(y+3))/(log(2))-1=x+1-1`
`(log(y+3))/(log(2))-1=x`

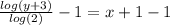
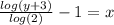
3. Swap variables:

`(log(y+3))/(log(2))-1=x+1-1`
`y=(log(x+3))/(log(2))-1`

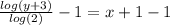
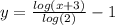
4. Rewrite it in this form:

`f^(-1)(x)=(log(x+3))/(log(2))-1`

Hence, the answer is:

`f^(-1)(x)=(log(x+3))/(log(2))-1`