Question

find the lateral area and surface area the lateral area of the prism is __in squared. the surface area of the prism is __ in squared

Answer 1

The lateral area of the prism is 900 in squared

The surface area of the prism is 960 in squared

Step-by-step explanation

Given:

The first side of the triangular base, a = 12 in

The second side of the triangular base, b = 13 in

The height of the prism, h = 30 in

What to find:

The lateral area and surface area of the prism.

Step-by-step solution:

The first step is to find the third side, c of the triangular base using Pythagoras rule.

`\begin{gathered} b^2=c^2+a^2 \\ \\ 13^2=c^2+12^2 \\ \\ c^2=13^2-12^2 \\ \\ c^2=169-144 \\ \\ c^2=25 \\ \\ c=√(25) \\ \\ c=5\text{ }in \end{gathered}`

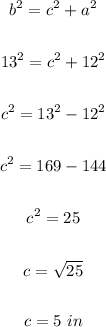
Now, the next step is to calculate the lateral area of the prism using the formula below.

`\begin{gathered} L.A=ha+hb+hc \\ \\ L.A=30*12+30*13+30*5 \\ \\ L.A=360+390+150 \\ \\ L.A=900\text{ }in^2 \end{gathered}`

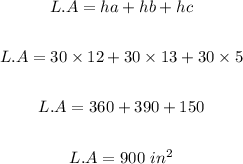
The lateral area of the prism is 900 in squared

The final step is to calculate the surface area of the prism using the formula below.

`S.A=Lateral\text{ }Area+Base\text{ }Area`

The base area is

`=2((1)/(2)cb)=2((1)/(2)*5*12)=2((60)/(2))=60\text{ }in^2`

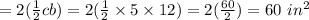
Therefore, the Surface Area = (900 + 60) = 960 in squared