Question

Find the functionFind the function that is finally graphed after the following transformations are applied to the graph of y=|x|. The graph is shifted right 3 units, stretched by a factor of 3, shifted vertically down 2 units, and finally reflected across the x-axis.Ay = -(3|x + 3| - 2)By = -(3|x - 3| - 2)Cy = 3|-x - 3| - 2Dy = -3|x - 3| - 2

Answer 1

`y=|x|`

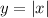
When the graph of parent function above is shifted 3 units right, the equation becomes:

`y=|x-3|`

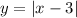
If it is stretch by a factor of 3, this means we will multiply the function by 3. The function becomes:

`y=3|x-3|`

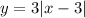
Then, if we add another transformation, that is shifted vertically down by 2 units then, this means, we will subtract 2 on the function. The function becomes:

`y=3|x-3|-2`

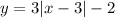
Finally, if the function is reflected across the x-axis, then we will multiply -1 to the entire function. The function becomes:

`y=-(3|x-3|-2)`

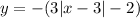
The answer is found in Option B.