Question

If you stand on top of a hill overlooking a lake and shout, how long is the lake if an echo is heard 2.0 s later on a day when the air temperature is 21°C?

Answer 1

343.5 m

Step-by-step explanation

Given:

• The time it takes the echo to return, t = 2s

,

• The temperature of the air, T = 21°C

We have to find the distance to the lake.

If we have the speed of sound, s, the distance to the lake, d, is traveled twice by the sound - to the lake and back. Thus, the speed is,

`s=(2d)/(t)`

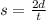
Solving for d,

`d=(s\cdot t)/(2)`

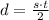
We don't know the speed of sound, but we know the temperature of the air. The speed of sound is given by,

`s=331m/s\cdot\sqrt[]{(T)/(273K)}`

Where T is the temperature in Kelvin. Transform the given temperature from degrees Celsius to Kelvin,

`T=21+273=294K`

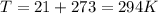
The speed of sound at this temperature is,

`s=331m/s\cdot\sqrt[]{(294K)/(273K)}\approx343.5m/s`

And the distance to the lake is then,

`d=(343.5m/s\cdot2s)/(2)=343.5m`

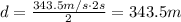
Hence, the distance to the lake is 343.5 m.