The coordinates of the vertices of a quadrilateral JKLM are given.
It is required that you translate 4 units to the left and 2 units up and match the graph that correctly shows the image J'K'L'M' after translation.
The given coordinates are:
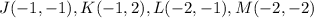
To translate 4 units to the left and 2 units up, subtract 4 from the x-coordinates and add 2 to the y-coordinates. (translation to the left is a subtraction, while translation upwards is addition):
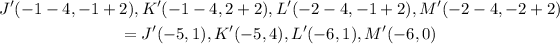
Compare the coordinates of the vertices of the image J'K'L'M' with the graphs given in the option.
The correct graph that shows the quadrilateral J'K'L'M' is: