Question

Alien scientists discover an asteroid headed directly towards their planet. The alien planet has a mass of M=6.39x1023 kg and the asteroid has a mass of m=1.50x108 kg. When the asteroid is a distance r1=3.40x108 m from the center of the alien planet, it has a velocity v1=1.00 m/s. The alien scientists calculate it will hit the surface of the planet with velocity v0=4982.00 m/s. What is the radius of the alien planet?

Answer 1

Given the mass of an alien planet,

and the mass of the asteroid is

`m=1.50*10^8\text{ kg}`

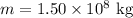
The asteroid has velocity v1 = 1 m/s when it is at a distance,

`r1=3.40*10^8\text{ m}`

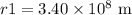
We have to find the radius,r, when it hits the surface with velocity v0 = 4982 m/s

In order to find the radius, we have to use the energy formula at two different distances,

one at radius r1 and the other at the radius r.

There are 2 types of energy, one is kinetic energy due to the motion of the asteroid and the other one is gravitational potential energy due to the alien planet.

So, total energy at distance, r1 is given by

`(1)/(2)m(v1)^2-(GMm)/(r1)\text{ ..}.(1)`

Here, G = 6.67 x 10^-11 m^3/Kg s^2 which is the universal gravitational constant.

Also, the total energy at the radius, r is given by

`(1)/(2)m(v0)^2-(GMm)/(r)\text{ ..}.(2)`

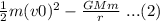
According to the conservation of energy, equations (1) and (2) are equal

`(1)/(2)m(v1)^2-(GMm)/(r1)=(1)/(2)m(v0)^2-(GMm)/(r)`

Rewriting the equation for radius,

`\begin{gathered} r=(GMm)/((1)/(2)m\mleft\lbrace(v0)^2-(v1)^2\)+\frac{\text{GMm}}{r1}\mright?} \\ =(GM)/((1)/(2)\mleft\lbrace(v0)^2-(v1)^2\mright\rbrace+(GM)/(r1)) \end{gathered}`

Substituting the values in the above equation, we get

`\begin{gathered} r=(4.2621*10^(13))/(12535518.2) \\ =3400018.996\text{ m} \\ =3.4*10^6\text{ m} \end{gathered}`

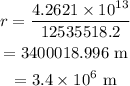
Hence the radius of the planet is 3.4x 10^6 m