We know that
• The mean is 750 hours.
,
• The standard deviation is 75 hours.
To find the probability between 900 and 975, we have to find
![P(900Remember that these probabilities fall into a normal distribution, where we can construct the intervals using the mean and the standard deviation.<p>So, we have to find the z-score for p(900) and p(975).</p>[tex]Z_(900)=(x-\mu)/(\sigma)=(900-750)/(75)=(150)/(75)=2]()
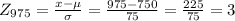
Now, we use these values in the following
![P(900Where each probability is found using the z-scores table, there you find that each probability is [tex]\begin{gathered} P(z<3)=0.9986 \\ P(z<2)=0.9772 \end{gathered}]()
We subtract
[tex]P(900To have it in percentage, we multiply by 100%[tex]P(900Therefore, the probability of selecting a light bulb that will last between 900 and 975 is 2.14%.