Question

The magnitude and direction of two forces acting on an object are 80 pounds, S65°E, and 100 pounds, N62°E, respectively. Find the magnitude, to the nearest hundredth of a pound, and the direction angle, to the nearest tenth of a degree, of the resultant force.Question content area bottomPart 1The magnitude is approximately enter your response here pounds. (Do not round until the final answer. Then round to the nearest hundredth as needed.)

Answer 1

By placing the vector as the hypotenuses of a right triangle we can see the distance can be broken up into two components (vertical and horizontal). These can be found with trig:

`\begin{gathered} vertical=80\cos (65)=33.809\rightarrow down \\ \text{horizontal}=80\sin (65)=72.504\rightarrow right \end{gathered}`

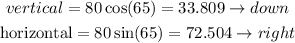
Doing the same for the other force we get:

`\begin{gathered} vertical=100\cos (62)=46.947\rightarrow up \\ \text{horizontal}=100\sin (62)=88.294\rightarrow right \end{gathered}`

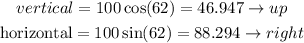
Adding up all vertical and horizontal we get:

`\begin{gathered} vertical\colon33.809+46.947=80.756 \\ \text{horizontal: 72.504+88.294=160.798} \end{gathered}`

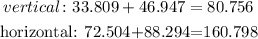
The magnitude is the hypotenuse. Therefore:

`\sqrt[]{80.756^2+160.798^2}=179.94`

Answer: 179.94 pounds