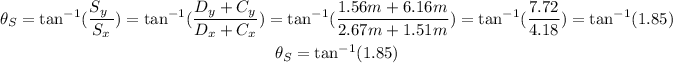Question

Vector C is 6.28 m long in a105° direction. Vector D is3.09 m long in a 233º direction.Find the direction of theirvector sum.

Answer 1

`\theta_S=\tan ^(-1)(1.85)=61.6069\text{ Deg}`

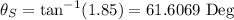
Step-by-step explanation: We need to find the resultant vector S that is the sum of the two vectors:

`\begin{gathered} C=C_x+C_y\Rightarrow\lvert C\rvert=\sqrt[]{(C_x)^2+(C_y)^2}=6.28m \\ \theta_c=\tan ^(-1)((C_y)/(C_x))=105^(\circ) \\ \text{ Likewise} \\ D=D_x+D_y\Rightarrow\lvert D\rvert=\sqrt[]{(D_x)^2+(D_y)^2}=3.09m \\ \theta_D=\tan ^(-1)((D_y)/(D_x))=233^(\circ) \\ \text{ We need to find: } \\ \theta_S=\tan ^(-1)((S_y)/(S_x))\rightarrow\text{ ?} \\ S_y\text{ }\rightarrow\text{?} \\ S_z\rightarrow? \\ \end{gathered}`

Next step is fairly easy, we just need to solve simultaneous equations, which will give us components of C D vectors, then finding the direction of vector sum would be the last step

`\begin{gathered} C=C_x+C_y\Rightarrow\lvert C\rvert=\sqrt[]{(C_x)^2+(C_y)^2}=6.28m \\ \theta_c=\tan ^(-1)((C_y)/(C_x))=105^(\circ)\rightarrow(C_y)/(C_x)=\tan (105^(\circ))\rightarrow C_y=C_x\tan (105^(\circ))=C_x4.03 \\ \therefore\rightarrow C_y=C_x4.03 \\ \text{ Now we can solve for the vector components from the above equation as:} \\ \sqrt[]{(C_x)^2+(C_y)^2}=6.28m\rightarrow\mleft(C_x\mright)^2+\mleft(C_y\mright)^2=(6.28m)^2 \\ (C_x)^2+(C_y)^2=(6.28m)^2\Rightarrow(C_x)^2(4.03)^2+(C_x)^2=(6.28m)^2 \\ (C_x)^2\lbrack(4.03)^2+1\rbrack=(6.28m)^2\rightarrow17.22(C_x)^2=39.44\rightarrow(C_x)^2=(39.44)/(17.22) \\ \therefore\rightarrow \\ C_x=\sqrt[]{(39.44)/(17.22)}=1.51m\rightarrow(1) \\ \therefore\rightarrow \\ (C_y)^2=(6.28m)^2-(C_x)^2=39.44m-1.51m=37.93m \\ C_y=\sqrt[]{37.93m}=6.16m\rightarrow(2) \\ \end{gathered}`

Similarly for D same thing as above is done, as shown next:

`\begin{gathered} D=D_x+D_y\Rightarrow\lvert D\rvert=\sqrt[]{(D_x)^2+(D_y)^2}=3.09m \\ \theta_D=\tan ^(-1)((D_y)/(D_x))=233^(\circ)\rightarrow(D_y)/(D_x)=\tan (233^(\circ)^{})\rightarrow D_y=D_x\tan (233^(\circ))=D_x0.58 \\ \therefore\rightarrow\text{ }D_y=D_x0.5 \\ \text{Now we can solve for the vector components from the above equation as:} \\ \sqrt[]{(D_x)^2+(D_y)^2}=3.09m\rightarrow(D_x)^2+(D_y)^2=(3.09m)^2 \\ (C_x)^2+(C_y)^2=(3.09m)^2\Rightarrow(D_x)^2(0.58)^2+(D_x)^2=(3.09m)^2 \\ \therefore\rightarrow \\ (D_x)^2\lbrack(0.58)^2+1\rbrack=(3.09m)^2\rightarrow1.34(D_x)^2=9.54\rightarrow(D_x)^2=(9.54)/(1.34) \\ \therefore\rightarrow \\ D_x=\sqrt[]{(9.54)/(1.34)}=2.67m\Rightarrow(3) \\ (D_y)^2=(3.09m)^2-(D_x)^2=9.55m-7.12m=2.43m \\ D_y=\sqrt[]{2.43m}=1.56m\Rightarrow(4) \end{gathered}`

Now the direction simply is:

`\begin{gathered} \theta_S=\tan ^(-1)(\frac{S_y\text{ }}{S_x_{}})=\tan ^(-1)((D_y+C_y)/(D_x+C_x))=\tan ^(-1)(\frac{1.56m_{}+6.16m_{}}{2.67_{}m+1.51m_{}})=\tan ^(-1)(\frac{7.72_{}}{4.18_{}})=\tan ^(-1)(1.85) \\ \theta_S=\tan ^(-1)(1.85) \end{gathered}`