Question

Your elderly neighbor places a bag of corn kernels on your doorstep each morning. The first day, the bag contained 1 kernel of corn, the second day it contained 2 kernels of corn, 4 kernels of corn the third day, and so on. Each kernel of corn weighs 0.07 grams. How much will the contents of the bag weigh on the 26th day? Round your answer to the nearest hundredth, if necessary.

Answer 1

The given information is:

-The bag contained 1 kernel of corn the first day.

-The bag contained 2 kernels of corn the second day.

-The bag contained 4 kernels of corn the third day.

-Each kernel of corn weighs 0.07 grams.

As can be observed, the number of kernels of corn doubles each day.

Then, we can find a formula to find the number of kernels at day d.

The formula is given by:

`K(d)=a\cdot r^(d-1)`

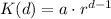
Where a is the kernel of corn on day 1, r is the rate of increase, which is 2 (it doubles) and d is the number of days.

Thus, on day 26, the values are a=1, r=2 and d=26. Replace these values and find K:

`\begin{gathered} K(26)=1\cdot2^(26-1) \\ K(26)=2^(25) \\ K(26)=33,554,432\text{ kernels} \end{gathered}`

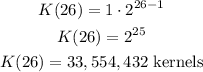
Now, as each kernel of corn weighs 0.07 grams, we need to multiply the number of kernels by this weight and find the total weight of the bag:

`33,554,432*0.07g=2348810.24`

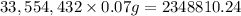
On the day 26th, the bag will weigh 2348810.24 grams.