Question

Determine if the given function us continuous at given value of x. Show the solution

Answer 1

The function is continuous if f(c) is defined, where c is a constant and the limit of x approach to c give the same value of f(c)

For the given function

`f(x)=(x^2)/(x-3)`

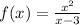
If f(-3) is defined, then the function is continuous at this value

Let us find f(-3) by substituting x by -3

`\begin{gathered} f(-3)=((-3)^2)/(-3-3) \\ f(-3)=(9)/(-6) \\ f(-3)=-(3)/(2) \end{gathered}`

Then f(-3) = -3/2

`\lim _(x\rightarrow-3)(x^2)/(x-3)=((-3)^2)/(-3-3)=(9)/(-6)=-(3)/(2)`

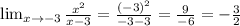
Since f(-3) has the same value of the limit of x approach to -3, then

The function is continuous at x = -3