We have that the practice line of Chloe is given by the second figure. Let us find what is the length that Chloe has for practice. We have a right triangle, and we also have the lengths of the legs of the triangle. We can apply here the Pythagorean Theorem to find the hypotenuse (Chloe zip line of practice). Then, we have:
![h^2=20^2+26^2^{}\Rightarrow h=\sqrt[]{20^2+26^2}\Rightarrow h=32.80ft](https://img.qammunity.org/2023/formulas/mathematics/college/h7ufsszptp12s8wepcmlrevg8fpunulnc8.png)
Now, let us find the side CD of the triangle ACD. We can apply the Law of Sines to solve for this side of the triangle:
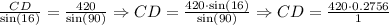
Then, the side CD is:

We can use the same Law of Sines to find the side AD. Since the inner sides of a triangle sum 180, we have that the angle < DCA = 74:
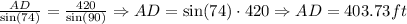
We now can apply the Law of Sines again to find BD:
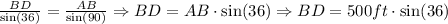
Then, we have:
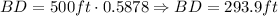
We can calculate the angle E from the practice line of Chloe. We can also apply the Law of Sines:
We already calculated the hypotenuse of this triangle before, and the length is equal to 32.80ft, then we have:
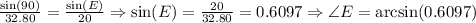
Then, we have that:
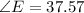
This angle value is near the measure of the angle of Daredevil's zip line.
From the comparison of the triangles, we can see that the Daredevil triangle is almost similar to that of the triangle used by Chloe to practice. We have that they have similar angles and the proportions of the sides are:
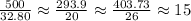
The Beginner's triangle is not a similar triangle to that of the triangle used by Chloe, the angles are not similar, and the sides do not have the same proportion to that of Chloe's practice.
Therefore, Daredevil's line is closest to Chloe's practice zip line because the triangles used in each case present almost the same ratio, and all the sides and angles have a similar proportion. Then, Chloe practices on a similar zip line. The Beginner's zip line is not similar to that of Chloe's zip line practice.