Question

Over the last three evenings,Rachel received a total of 87 phone calls at the call center. The first evening, she received 9 fewer calls than the second evening. The third evening, she received 2 times as many calls as the second evening. How many phone calls did she receive each evening?Solve by using linear equation

Answer 1

Let's use the variables x, y and z to represent the number of phone calls received in the first, second and third evening.

The total number of phone calls received is 87, so we have:

`x+y+z=87`

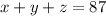
On the first evening, the number of phone calls is 9 fewer than the number on the second evening, so:

`x=y-9`

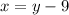
On the third evening, the number of phone calls is 2 times the number on the second evening, so:

`z=2y`

Using these values of x and z in the first equation, we have:

`\begin{gathered} (y-9)+y+(2y)=87 \\ 4y-9=87 \\ 4y=87+9 \\ 4y=96 \\ y=(96)/(4) \\ y=24 \end{gathered}`

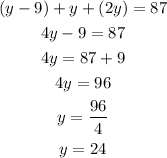
Now, solving for x and z, we have:

`\begin{gathered} x=y-9=24-9=15 \\ z=2y=2\cdot24=48 \end{gathered}`

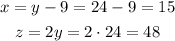
Therefore Rachel received 15 calls on the first evening, 24 calls on the second evening and 48 calls on the third evening.