Question

O GRAPHS AND FUNCTIONSWord problem involving average rate of change

Answer 1

Given:

a)

we get the points (2,71.2) and (4,166.4) from the table.

Consider the rate of change

`\text{Rate of change =}(y_2-y_1)/(x_2-x_1)`
`\text{ Substitute }y_2=166.4,y_1=71.2,x_2=4\text{ and }x_1=2,\text{ we get}`

`\text{Rate of change =}(166.4-71.2)/(4-2)`

`\text{Rate of change =}47.6\text{ meters per second.}`

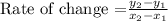
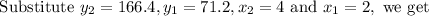
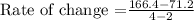
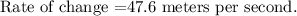
The average rate of distance for the distance from 2 seconds to 4 seconds is 47.6 meters per second.

b)

We get the points (6,172.8) and (10, 239.6) from the table.

`\text{Rate of change =}(y_2-y_1)/(x_2-x_1)`

`\text{ Substitute }y_2=239.6,y_1=172.8,x_2=10\text{ and }x_1=6,\text{ we get}`

`\text{Rate of change =}(239.6-172.8)/(10-6)`

`\text{Rate of change =}16.7\text{ meters per second.}`

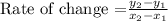
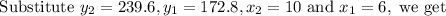
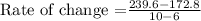
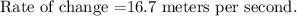
The average rate of distance for the distance from 6 seconds to 10 seconds is 16.7 meters per second.