Question

10. The shortest side of a similar triangle is 15. Find the perimeter of the The sides of a triangle measure 6,8, and larger triangle.

Answer 1

If the sides of a triangle are 6,8 and 10, and if we know that the shorter side of a similar triangle is 15 the we know that the this relation has to be true so:

`(15)/(6)=(x)/(8)=(y)/(10)`

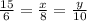
So we can find x and y that are the missing sides of the similar triangle so:

`\begin{gathered} (x)/(8)=(15)/(6) \\ x=(15\cdot8)/(6) \\ x=20 \end{gathered}`

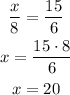
and for y:

`\begin{gathered} (y)/(10)=(15)/(6) \\ y=(15\cdot10)/(6) \\ y=25 \end{gathered}`

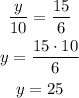
So the perimeter (P) will be:

`\begin{gathered} P=15+20+25 \\ P=60 \end{gathered}`