Question

Find the missing side in each triangle using any method. Check your answer using a different method.

Answer 1

Step-by-step explanation:

Triangle ABC is similar to triangle FED

Using similar triangles theorem:

The ratio of corresponding sides are equal

AC corresponds to FD

AB corresponds to FE

BC corresponds to ED

AC/FD = AB/FE = BC/ED

AC/26 = 5/10 = 12/ED

solving for AC:

`\begin{gathered} (AC)/(26)=(5)/(10) \\ \text{cross multiply:} \\ 10(AC)\text{ = 26(5)} \\ 10AC\text{ = 130} \\ AC\text{ = 130/10} \\ AC\text{ = 13} \end{gathered}`

5/10 = 12/ED

`\begin{gathered} (1)/(2)=(12)/(ED) \\ 1(ED)\text{ = 2(12)} \\ ED\text{ = 24} \end{gathered}`

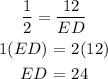
To check our answer we are asked to use another method

Using pythagoras' theorem:

Hypotenuse² = opposite² + adjacent²

For ABC:

AC² = 12² + 5²