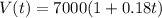This are simple interest situations.
THe equation for simple interest is:
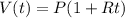
Where
t is the time in years
V(t) is the total, the principal amount plus interest
R is the rate of interest
P is the principal value, the amount initially.
in the first case, we have
P = $7000
R = 9% every year
we need to convert it to decimal: 9% / 100 = 0.09
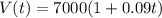
For the second situation:
P = $7000
R = 9% every 7 years
Then, we first convert 9% to decimal: 0.09 and divide it by 7, because we want to express it by t = numer of years.
0.09 / 7 = 9/700
Then equation fo the second case:
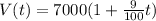
If you The last case:
P = $7000
R = 9% every 1/2 year.
9% to decimal: 0.09 and since this is what the value increases half a year, in a year increases twice, 2 · 0.09 = 0.18