Question

Find the value of c such that each expression is a perfect square trinomial

Answer 1

2. The given expression is;

`z^2+2z+c`

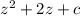
We want to make the expression a perfect square trinomial.

In other words, we want to "complete the square".

In order to complete the square, we need to make c to be equal to

the square of the coefficient of the first power term divided by twice the coefficient of the first power term.

In other words,

`c=((b)/(2a))^2`

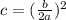
Here, b =2 and a =1, so;

`c=((2)/(2*1))^2=1`

Therefore, the value of c to be added to make the expression a perfect square is 1

4. We have to find c;

`p^2-11p+c`

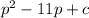
We know that; a = 1 and b = -11 , so ;

`\begin{gathered} c=((b)/(2a))^2=((-11)/(2))^2 \\ c=30.25 \end{gathered}`

Therefore, the value of c to be added to make the expression a perfect square is 30.25