Given that the mass of the ball is m1= 0.75 kg and initial velocity, u1 = 21 m/s.
This ball strikes a bottle of mass, m2= 0.5 kg, and the initial velocity of the bottle, u2 = 0 m/s.
We have to find the final velocity of the ball, v1 after collision with the bottle having final velocity, v2 = 20 m/s
Momentum is conserved during a collision. So, the equation of momentum can be written as
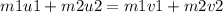
Substituting the values, v1 will be
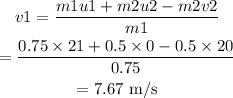
Thus, the velocity of the ball is 7.67 m/s.