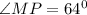
And it is the angle at the centre of a circle
The theorem,
Angle at the centre of a circle = 2 x angle at the other part of the circumference
Hence;
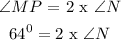
Divide both sides by 2
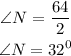
Part B:
We are to find the angle at the centre in this case
The angle at the centre is NQ and P is the angle at the circumference
Applying the same theorem as we used in part A, that is
Angle at the centre of a circle = 2 x angle at the other part of the circumference
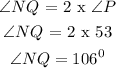
Hence, angle N = 32 degrees and angle NQ = 106 degrees.