Given:
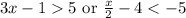
To find the solutions for this compound inequality, we will first need to solve for x.
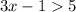
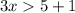
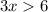
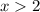
Since x > 2, this would give us an interval notation of ( 2, ∞ )
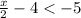
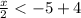
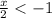

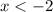
Now, since x < -2, this will give us an interval notation of ( -∞, -2 )
Since we see the word OR in our compound inequality, this would mean that the solution for this is ( -∞, -2 ) ∪ ( 2, ∞ )