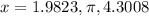We can see that the expression is a quadratic expression of the form:
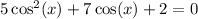
Now we can say:
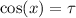
And use the quadratic equation:
![\begin{gathered} 5\tau^2+7\tau+2=0 \\ \tau_(1,2)=\frac{-7\pm\sqrt[]{7^2-4\cdot5\cdot2}}{2\cdot5}=\frac{-7\pm\sqrt[]{49-40}}{10}=(-7\pm3)/(10) \\ \tau_1=(-7+3)/(10)=-(4)/(10)=-(2)/(5) \\ \tau_2=(-7-3)/(10)=-(10)/(10)=-1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/vgzh754zd3zrqj33pbyeozjoei0s4kiwhe.png)
The solutions are the values of x such:
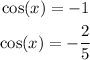
We know that if x = π, cos(x) = -1. Thus, π is a solution.
The other solutions are:
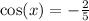
And since cos has a period of 2π, the solutions are:
The two other solutions for [0, 2pi) are:
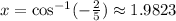
And:

All the solutions in the interval are: