Question

Logarithm 8) if 2/ log20-1 = logbA, find the value of A and B

Answer 1

Hello there. To solve this question, we'll have to apply some logarithm properties to rewrite the number and determine the values of A and B.

Given

`(2)/(\log (20)-1)=\log _B(A)`

We can rewrite the expression in the denominator using the following rule:

`\log _C(a)-\log _C(b)=\log _C\left((a)/(b)\right)`

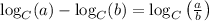
Remember that we write log for a logarithm with base 10 and ln for a logarithm with base e, thus we have:

`\log (20)-1=\log (20)-\log (10)=\log \mleft((20)/(10)\mright)=\log (2)`

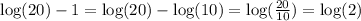
And rewrite the expression in the numerator using the property:

`\log _C(a^b)=b\cdot\log _C(a)`

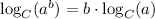
Therefore we have:

`2=2\cdot1=2\cdot\log (10)=\log (10^2)=\log (100)`

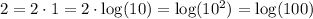
Finally, we use the following property to find A and B:

`(\log_C(a))/(\log_C(b))=\log _b(a)`

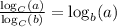
We get that:

`(\log(100))/(\log(2))=\log _2(100)`

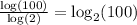
And this is equal to:

`\log _2(100)=\log _B(A)`

If only A = 100 and B = 2.