Step 1:Write out the coordinates of the vertices of the objects and its images
Let the vertices of R be ABCD such that
A ( -9 , 3) B ( -5 , 7) C (-3 , 5) D (-5 , 2)
Let the vertices of R' be A'B'C'D' such that
A' (9 ,-6) B' (5 , -2) C' (3 , -4) D' (5 , -7)
Step 2: Reflect the object R about the y-axis
The reflection rule about the y-axis is given by
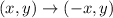
Let the corresponding image of R after reflection about the y-axis be the quadrialteral A'B'C'D'. Hence,
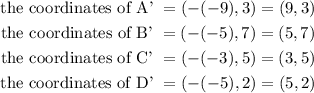
Step 3: Translate the quadrilateral A'B'C'D' down by 9 units.
The rule for translation down by 9 units is given by
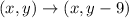
Let the corresponding image of A'B'C'D' after translation down the y-axis be the quadrialteral A''B''C''D''.
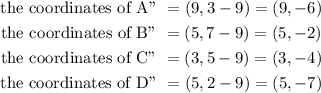
Hence, the coordinates of the vertices of the quadrialteral A''B''C''D'' corresponds to the coordinates of the vertices of R' .
Therefore, a translation 9 units down followed by a reflection over the y -axis, Option A is the correct answer