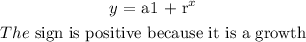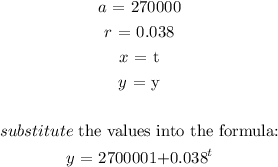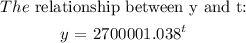Question

At the beginning of a population study, a had 270.000 people. Each year since, the population has grown by 3.8% Let be the number of years since start of the study. Let be the city's population. Write an exponential function showing the relationship between y and

Answer 1

Answer:
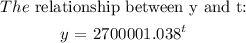
`\begin{gathered} The\text{ relationship between y and t:} \\ y\text{ = 270000\lparen1.038\rparen}^t \end{gathered}`Step-by-step explanation:

Given:

Initial population = 270000

rate of growth per year = 3.8% = 0.038

t = number of years

y = city's population

To find:

the exponential function showing the relationship between y and t

To determine the relationship, we will apply the exponential function formula:

`\begin{gathered} y\text{ = a\lparen1 + r\rparen}^x \\ The\text{ sign is positive because it is a growth} \end{gathered}`
`\begin{gathered} a\text{ = 270000} \\ r\text{ = 0.038} \\ x\text{ = t} \\ y\text{ = y} \\ \\ substitute\text{ the values into the formula:} \\ y\text{ = 270000\lparen1+0.038\rparen}^t \end{gathered}`
`\begin{gathered} The\text{ relationship between y and t:} \\ y\text{ = 270000\lparen1.038\rparen}^t \end{gathered}`