The system of equations we have is:
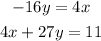
Step 1. Substitute the first equation into the second equation.
We substitute the value of 4x by the value of -16y:
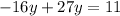
Step 2. Solve the previous equation for y.
We add the like terms in the left side of the equation:
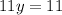
Step 3. Divide both sides of the equation by 11:
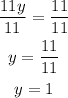
Step 4. Now that we know that y=1, we substitute this value into the first equation of the system of equations:
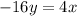
since y=1, we get:
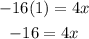
Step 5. Divide both sides of the equation by 4:
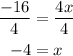
Step 6. Write the solution as an ordered pair.
We remember than an ordered pair has the general form:
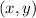
The first number is always the x value, and the second number is always the y value.
Since in this case, we have:
x=-4
and
y=1
The ordered pair will be:
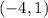
Answer: (-4,1)