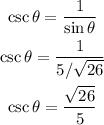Question

The terminal side passes through (-5,1). Find sin 0, cos 0, tan 0, csc 0, sec 0, and cot 0.

Answer 1

The terminal side of an angle passes through (-5, 1).

The angle is located at quadrant II, as shown below:

The tangent of the angle is defined as:

`\tan\theta=(y)/(x)`

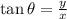
Calculating:

`\tan\theta=(-5)/(1)=-5`

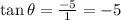
The cotangent is the reciprocal of the tangent, thus:

`\cot\theta=(1)/(-5)=-(1)/(5)`

We can find the secant by using the equation:

`\sec^2\theta=1+\tan^2\theta`

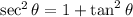
The secant is negative in quadrant II, so we use the negative root:

`\begin{gathered} \sec^\theta=-√(1+\tan^2\theta) \\ \sec\theta=-√(1+(-5)^2) \\ \sec\theta=-√(26) \end{gathered}`

The cosine is the reciprocal of the secant, thus:

`\begin{gathered} \cos\theta=(1)/(\sec\theta) \\ \cos\theta=-(1)/(√(26)) \end{gathered}`

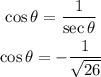
The sine can be calculated in several ways. We use, for example:

`\begin{gathered} \sin\theta=\tan\theta\cos\theta \\ \sin\theta=-5*(-(1)/(√(26))) \\ \sin\theta=(5)/(√(26)) \end{gathered}`

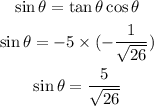
Finally, the cosecant is the reciprocal of the sine:

`\begin{gathered} \csc\theta=(1)/(\sin\theta) \\ \csc\theta=(1)/(5/√(26)) \\ \csc\theta=(√(26))/(5) \end{gathered}`