Question

For problems 6-9, determine which lines, if any, can be proven parallel using the given information andfind the transversal that cuts the parallel lines. Justify your answer using an angle pair converse.6.41 = 45m7.43 24138. 41 41113 11614/159/1210/11P9. 416 and 49 are supplementary

Answer 1

POSTULATES:

If two lines are cut by a transversal and corresponding angles are congruent, then the lines are parallel.

QUESTION 6:

`\angle1\cong\angle5`

The two angles are corresponding angles, on Line m. Therefore,

Parallel lines: j and k

Transversal: m

QUESTION 7:

`\angle3\cong\angle13`

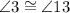
The two angles are interior opposite angles located on the line j. Therefore,

Parallel lines: m and p

Transversal: j

QUESTION 8:

`\angle1\cong\angle11`

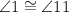
The two angles are not corresponding. However, we can see that:

`\begin{gathered} \angle1\cong\angle3\text{ (}vertical\text{ angles)} \\ \angle3\cong\angle15\text{ (corresponding angles)} \\ \angle15\cong\angle11\text{ (corresponding angles)} \end{gathered}`

This proves our initial postulate.

QUESTION 9:

`\angle16\text{ and }\angle9\text{ are supplementary}`

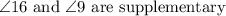
If two parallel lines are cut by a transversal, then the interior angles on the same side of the transversal are supplementary angles.

Therefore,

Parallel lines: j and k

Transversal: p