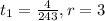Given:
A geometric sequence with sixth term '4' and tenth term '324'.
Required: First term and common ratio
Step-by-step explanation:
The general term of a geometric sequence is
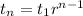
Since the sixth term is 4,
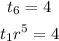
Since the tenth term is 324,
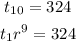
Dividing them.

Substitute 3 of r into t6 =4.
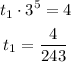
Substitute -3 of r into t6 =4.
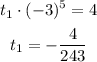
There are two possible geometric sequences:
1) First term, t1 = -4/243 and common ratio, r = -3
2) First term, t1 = 4/243 and common ratio, r = 3.
The correct option is option (b)
Final Answer: