Step-by-step explanation
From the statement, we know that:
• ∠ABC ≅ ∠EFG,
• ∠ABC = (4x + 3)°,
• ∠EFG = (2x + 11)°.
(1) Using the data from above, we have:
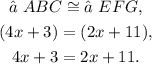
(2) Solving for x the last equation:
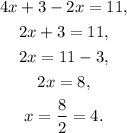
(3) Replacing the value x = 4 in the equations of the first angle, we get:
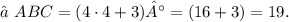
Answer
m∠ABC = m∠EFG = 19°