Given the expression in the image, we first get the resulting fraction from the calculations though the following steps.
Step 1: We factorise the 4 quadratic equations:
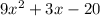
Factors of the equation above after factorisation will be;
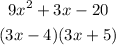
Equation 2:
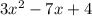
Factors of the equation above after factorisation will be;
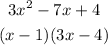
Equation 3:
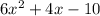
Factors of the equation above after factorisation will be;
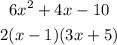
Equation 4:
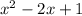
Factors of the equation above after factorisation will be;
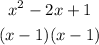
Step 2: To compute the division, we have
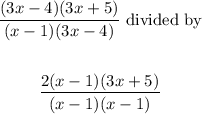
We have:
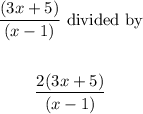
This gives us:
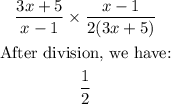
From the final fraction which is 1/2, it can be seen that the numerator is 1 while the denominator is 2.