Question

Kayla and John are reading a graphic novel. Kayla has read 45 pages and is now reading 30 pages per day. John has read 85 pages and is now reading 10 pages per day. Let x be the number of days and y be the total number of pages read.A. Write an equation in slope intercept form to the pages kayla has read. B. Write an equation in slope intercept form to the pages John has read. Let x ve the number of pages and y be the total number of pages read.C. How long will it be before Kayla and John have read the same number of pages?

Answer 1

Kayla has already read 45 pages.

Kayla is reading at a rate of 30 pages per day.

John has already read 85 pages.

John is reading at a rate of 10 pages per day.

Their equations can be modeled with

`y=mx+b`

Where m is the slope and b is the y--intercept

Here,

m is the rate at which they are reading per day

b is the amount of pages they have already read

Thus,

A.

Kayla's equation:

m = 30

b = 45

So,

`y=30x+45`

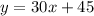
B.

John's equation:

m = 10

b = 85

So,

`y=10x+85`

C.

We need to find the number of days, x, when both have read same amount of pages (which is y). Thus, we equate the expressions for both y's and find x using algebra. Shown below:

`\begin{gathered} 30x+45=10x+85 \\ 30x-10x=85-45 \\ 20x=40 \\ x=(40)/(20) \\ x=2 \end{gathered}`

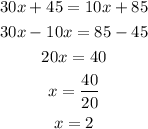
After 2 more days, the total number of pages of both Kayla and John would be equal!