Question

Hi, can you help me answer this question please, thank you!

Answer 1

z = 0.33

Step-by-step explanation:

The test statistic z can be calculated as:

`z=(p^(\prime)-p)/(\sigma)`

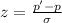
Where p' is the proportion of the sample and p is the value in H0. Additionally, σ is equal to:

`\sigma=\sqrt[]{(p(1-p))/(n)}`

Where n is the size of the sample.

In this case, we have a sample of 136 subjects, so n = 136 and taking into account H0, p = 0.42. So, replacing the values, we get:

`\begin{gathered} \sigma=\sqrt[]{(0.42(1-0.42))/(136)} \\ \sigma=0.0423 \end{gathered}`

Then, p' is the proportion of the sample, so it is equal to:

p' = 59/136 = 0.4338

Now, replacing p' = 0.4338, σ = 0.0423 and p = 0.42, we get that the test statistic is:

`z=(0.4338-0.42)/(0.0423)=0.33`

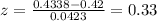
Therefore, the answer is:

z = 0.33