We need to match each general form of a function to the name.
• In a linear function, the exponent of the variable x is 1. Thus, it has the general form:

where m and b are constants.
• In a quadratic function, there is at least one term for which x has exponent 2. Thus, it has the general form:

where a, b, and c are constants, and a ≠ 0.
• In an exponential function, x is the exponent of a constant. Thus, its general form is:
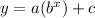
where a, b, and c are constants.
Answer: