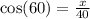Question

Select the equation that can be used to solve for x.

Answer 1

To solve this problem we need to remember the definitions of the trigonometric identities. For a given angle "m" in a right triangle, the sine (sin), cosine (cos), and tangent (tan) are defined as follows:

`\begin{gathered} \sin m=\frac{\text{opposite side}}{\text{hypotenuse}} \\ \cos m=\frac{\text{adjacent side}}{hypotenuse} \\ \tan m=\frac{opposite\text{ side}}{adjacent\text{ side}} \end{gathered}`

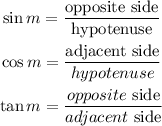
All of the options have x/40 on the right-hand side, so we need to find the correct trigonometric identity that is represented by x/40.

For the angle of 60°, 40 is the opposite side, and x represents the adjacent side.

Thus, the sine of 60 according to the definitions is:

`\begin{gathered} \sin m=\frac{\text{opposite side}}{\text{hypotenuse}} \\ \sin 60=(40)/(x) \end{gathered}`

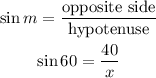
And the cosine of 60 according to the definition is:

`\begin{gathered} \cos m=\frac{\text{adjacent side}}{hypotenuse} \\ \cos 60=(x)/(40) \end{gathered}`

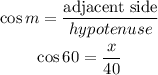
As you can see, sin60=40/x is not amongst the options. But cos60=x/40 is the fourth option.

Answer:

`\cos (60)=(x)/(40)`