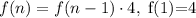Question

A) f(n) = f(n-1).4; f(1) = 4b) f (n) = 4n +1c) f(n) = f(n-1) +4; f(1) = 4d) f(n) = 1.4"

Answer 1

In Step 1, we have 4 dots. Therefore: f(1)=4

In Step 2, we have 16 dots. Therefore: f(2)=16

In Step 3, we had 64 dots. Therefore: f(3)=64

We observe that each of the f(n) is 4 raised to the particular n.

`\begin{gathered} f(1)=4^1=4 \\ f(2)=4^2=16 \\ f(3)=4^3=64 \end{gathered}`

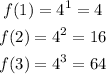
Therefore, the next term is obtained through the multiplication of the previous term by 4.

Therefore, the recursive formula which fits the dot will be:

`f(n)=f(n-1)\cdot4,\text{ f(1)=4}`