Question

Let x equals negative 31 times pi over 6 periodPart A: Determine the reference angle of x. Part B: Find the exact values of sin x, tan x, and sec x in simplest form.

Answer 1

An angle's reference angle is the measure of the smallest, positive, acute angle t formed by the terminal side of the angle t and the horizontal axis.

Given the value of x to be

`x=(-31\pi)/(6)`

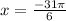
To get the reference angle of x, we will need to add an even multiple of pi to x

So we will have

`6\pi+(-(31\pi)/(6))=(5\pi)/(6)`

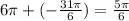
We have the reference angle to be:

`(5\pi)/(6)`

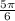
Part B

To find sin x

we will have

`\begin{gathered} \\ \sin x=\sin (5\pi)/(6)=(1)/(2) \\ \text{Therefore } \\ \sin x=(1)/(2) \end{gathered}`

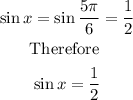
Similarly, we will have tan x to be

`\begin{gathered} \tan x=\tan (5\pi)/(6)=-\frac{\sqrt[]{3}}{3} \\ \end{gathered}`

For sec x

`\begin{gathered} \sec x=(1)/(\cos x) \\ so\text{ let us check cos x} \\ \cos x=\cos (5\pi)/(6)=-\frac{\sqrt[]{3}}{2} \\ \\ \text{Next,}we\text{ can compute} \\ \sec x=(1)/(\cos x)=\frac{1}{-\frac{\sqrt[]{3}}{2}}=-\frac{2}{\sqrt[]{3}} \end{gathered}`

Simplifying further

`\sec x=\frac{-2\sqrt[]{3}}{3}`