We need to compare the rates of change of the functions shown.
The rate of change of a linear function is the change in the y-coordinates divided by the corresponding change in the x-coordinates between two points.
The rate of change for the graphed function can be calculated using points A and B, for example. We obtain:
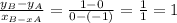
Notice that the first two rows of the table represent exactly points A and B: A(-1,0) and B(0,1). Thus, the rate of change will be the same:

Answer: The rates of change are equal.