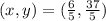Question

Find the point on the curve y=2x+5 closest to the point (0,8).

Answer 1

step 1

we have the curve

`y=2x+5`

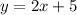
Find out the derivative

`y^(\prime)=2\text{ ----slope of the curve}`

step 2

Find out the equation of the line perpendicular to the given curve that passes through the point (0,8)

Remember that

If two lines are perpendicular, then their slopes are negative reciprocal

so

The slope of the perpendicular line is m=-1/2

The equation of the line is given by

`y=mx+b`

where

m=-1/2

point (0,8) ----> y-intercept

substitute

`y=-(1)/(2)x+8`

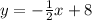
step 3

Find out the intersection of both lines

`\begin{gathered} y=2x+5 \\ y=-(1)/(2)x+8 \end{gathered}`

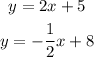
Equate both equations

`\begin{gathered} 2x+5=-(1)/(2)x+8 \\ 2x+(1)/(2)x=8-5 \\ \\ (5)/(2)x=3 \\ \\ x=(6)/(5) \end{gathered}`

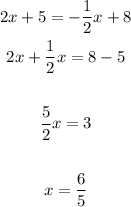
Find out the y-coordinate of the point

`\begin{gathered} y=2((6)/(5))+5 \\ \\ y=(12)/(5)+5 \\ \\ y=(37)/(5) \end{gathered}`

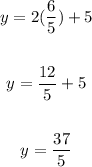
The coordinates of the point are

`(x,y)=((6)/(5),(37)/(5))`