Given the equation:
7x - 4y = -16
Let's find the slope and the y-intercept of the line.
Apply the slope-intercept form of a linear equation:
y = mx + b
Where m is the slope and b is the y-intercept.
Now, rewrite the equation for y using the following steps:
• Subtract 7x from both sides of the equation:
7x - 7x - 4y = -7x - 16
-4y = -7x - 16
• Divide both all terms in the equation by -4:
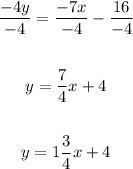
Therefore, the equation in slope intercept form is:

Thus, we have:
The slope of the line in its simplest form is = 1¾
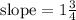
The y-intercept of the line is = 4
ANSWER:
Slope = 1¾
y-intercept = 4