You have that y varies directly with x, it means tha you can write the relation between both variables as follow:
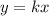
where k is the constant of proportionality.
If y = 3.15 when x = 9, you can find the value of k, just as follow:
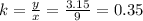
Then, the equation that relates y and x can be writen as follow:
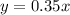
or
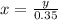
Now, you can find the value of x when y = 49, by replacing this value into the previous equation:
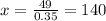
Hence, the value of x when y = 49 is x = 140