Answer:
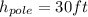
Step-by-step explanation: We have to find the height of the pole, which is just an opposite side of a triangle, we would have to resort to the pythagorean theorem and one of the trigonometric ratios, this is done as follows:
![\begin{gathered} \text{ Base is determined through pythagorean theorem:} \\ \Rightarrow a^2+b^2=c^2\rightarrow a=b \\ \therefore\rightarrow \\ 2a^2=27^2\Rightarrow a=b=\frac{27}{\sqrt[]{2}}=\frac{27\sqrt[]{2}}{2} \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/k45fcvtoccozb4mcu8rfnr1xm7j9aj6fos.png)
Height of the pole:
![\begin{gathered} \tan (57^(\circ))=\frac{Opposite\text{ }}{\text{Adjacent}}=(h)/(b)=\frac{h}{(\frac{27\sqrt[]{2}}{2})} \\ \tan (57^(\circ))=\frac{2h}{27\sqrt[]{2}}\rightarrow h=\frac{27\sqrt[]{2}}{2}\tan (57^(\circ))=\frac{27\sqrt[]{2}}{2}*(1.54)=29.40\cong30 \\ \therefore\rightarrow \\ h_(pole)=30ft \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/q90rx01f5rtbdgwtidy1yx7wo09omvzj5y.png)